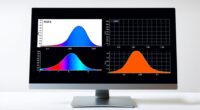
Z-scores are a useful way to standardize data, making it easier to compare scores across different tests or datasets. They transform data onto a common scale with a mean of 0 and a standard deviation of 1, regardless of original units. This helps you see how individual data points relate to the overall distribution, identify outliers, and enable fair comparisons. Keep exploring to understand how to apply z-scores effectively in your analyses.
Key Takeaways
- Z-scores convert different datasets onto a common scale, enabling direct comparison regardless of original units or measurement ranges.
- They standardize data by indicating how many standard deviations a data point is from the mean.
- Z-scores help identify outliers, highlighting data points that significantly deviate from the typical distribution.
- Using Z-scores simplifies statistical analyses like hypothesis testing and regression by normalizing data.
- They facilitate meaningful comparisons across variables and datasets, supporting data-driven decision-making.

Have you ever wondered how to compare scores from different tests or datasets? When dealing with data from varied sources, directly comparing raw scores can be misleading because each dataset might have different scales, units, or distributions. That’s where Z-scores come into play. They provide a way to standardize data, transforming different measurements onto a common scale. This process is crucial for meaningful comparisons and insightful analysis, especially when you’re trying to understand how individual data points relate to the overall dataset.
One of the key benefits of using Z-scores is their ability to assist with outlier detection. Outliers are data points that markedly deviate from the rest of the dataset. They can result from measurement errors, data entry mistakes, or genuine rare events. By converting raw scores into Z-scores, you can easily identify these anomalies, as outliers will have Z-scores far from zero, typically exceeding |3| in magnitude. This standardization helps you quickly pinpoint unusual observations that might distort your analysis or warrant further investigation.
Data normalization is another critical aspect of Z-scores. Normalization involves adjusting data to enable fair comparisons across different scales or units. When you normalize data, you’re essentially rescaling it so that each dataset conforms to a standard distribution with a mean of zero and a standard deviation of one. This process removes the influence of differing units or measurement ranges, allowing you to compare datasets directly. For example, if one test scores range from 0 to 100 and another from 200 to 800, raw scores alone don’t offer a fair comparison. But once you compute Z-scores, both datasets are normalized, making it straightforward to analyze performance across tests or groups.
Using Z-scores also simplifies statistical analysis. Many techniques, such as hypothesis testing or regression analysis, assume data follows a normal distribution or are easier to interpret when standardized. By converting scores into Z-scores, you align your data with these assumptions, increasing the accuracy of your results. Also, since Z-scores are dimensionless, they facilitate comparisons across variables that originally had different units, enhancing clarity and interpretability.
Additionally, understanding the distribution of your data through Z-scores can help inform decisions in various fields like education, finance, or healthcare, where analyzing data patterns is vital.
Frequently Asked Questions
How Do Z-Scores Relate to Probability Distributions?
You can use z-scores to relate data points to probability distributions by mapping their position within the distribution. When you calculate a z-score, you’re standardizing data, making it easier to compare different distributions. This process helps you see how far a value is from the mean concerning standard deviations, facilitating distribution comparison and probability mapping, especially when analyzing normal distributions and evaluating the likelihood of specific outcomes.
Can Z-Scores Be Negative, and What Do They Signify?
Imagine a compass pointing toward your data’s story. Yes, your z-scores can be negative, acting like a downward arrow indicating a value below the mean. Negative z scores symbolize data points that are less than average, helping you interpret their position within the distribution. They’re essential for understanding how far and in which direction your data deviates from the mean, guiding your analysis with clear z-score interpretation.
Are Z-Scores Applicable in Non-Normal Data?
You can use z-scores with non-normal data, but they might not always be reliable. When data isn’t normal, consider robust alternatives like percentile ranks or non-parametric methods, which don’t assume a specific distribution. These methods provide more accurate insights for skewed or irregular data, ensuring your analysis remains meaningful even when traditional z-scores fall short. Always evaluate your data’s distribution before choosing the most appropriate standardization technique.
How Do Sample Size and Variability Affect Z-Scores?
You should know that sample size effects and variability impact how z-scores are interpreted. A larger sample size typically leads to more reliable z-scores, reducing the influence of outliers. Higher variability, however, increases the standard deviation, which can decrease the z-score’s magnitude for a given data point. So, when variability is high, your z-scores might appear less extreme, affecting how you compare different data sets.
What Are Common Mistakes When Calculating Z-Scores?
You might make z score miscalculations by using an incorrect standard deviation, such as confusing sample and population values. Double-check that you’re using the right mean and standard deviation for your data set. Avoid errors like mixing up formulas or forgetting to subtract the mean from your data point. These mistakes can lead to inaccurate z-scores, which can skew your analysis and conclusions.
Conclusion
Just like the legendary Icarus aimed for the sun, using z-scores helps you rise above raw data’s chaos. By standardizing your data, you gain clarity and insight, making comparisons effortless—no matter the scale. Remember, with z-scores, you’re charting your course through the data universe, turning complexity into simplicity. Embrace this tool, and you’ll navigate your analysis with confidence, reaching new heights in understanding just as Icarus dreamed of soaring higher.